
Last weekend I went to play a reality room escape game with some friends. It’s a lot of fun and we finally escape on time!
The only thing make it less perfect is that we skip a “very hard” puzzle according to the staff in the room. We spend 1O minutes on it and we could not found an effective way to solve it.
The game is consisted of a board with 5 rows * 5 columns = 25 lights. Each light is either on or off. Player could switch any light on/off, but switching any light will also switch it’s neighbour on up/down/left/right position at the same time. The goal of this game is for a given status, try to switch some of the lights to make all the lights on.
You could also refer to this graph for the “switch logic”.
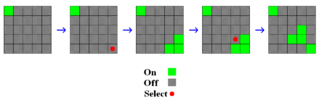
To win the game, For example, if the initial status looks like the following board (O mean an enlighted light and X mean an off light), then we could switch 2 lights on (2,1) and (4,3) to make all the light on. But is there an systematic way to get a solution?
| x | O | O | O | O | O | O | O | O | O | O | O | O | O | O | ||
| x | x | O | O | O | O | O | O | O | O | O | O | O | O | O | ||
| x | O | x | O | O | switch (2,1) => | O | O | x | O | O | switch (4,3) => | O | O | O | O | O |
| O | x | x | x | O | O | x | x | x | O | O | O | O | O | O | ||
| O | O | x | O | O | O | O | x | O | O | O | O | O | O | O |
But not all cases are so straight forward. For example:
| x | O | O | O | O | O | O | O | O | O | O | O | O | O | O | ||
| x | O | O | O | O | O | O | O | O | O | O | O | O | O | O | ||
| x | O | O | O | O | OR | O | O | O | O | O | OR | O | O | O | O | O |
| O | O | O | O | O | O | O | x | O | O | O | O | O | O | O | ||
| O | O | O | O | O | O | O | x | O | O | X | O | O | O | X |
Some Helpful Deduction
Before we further illustrate, there are 2 useful tips deduced from the game rule:
- we don’t need to switch a light for more than 1 time.
- the sequence of switching does not matter.
Solution 1: Brutal Enumeration
We enumerate all possible combination of switches based on the current status. And see whether there is possible solution. Base on the above deduction, this solution have a time complexity of $O(2^{mn})$, where m * n is the total number of lights.
Calculation will be effective if m,n < 5. But for a square grid with m = n = 6, it’s already quite a long time for a laptop.
Solution 2: Linear Algebra Way
The following linear algebra approach is a more systematic way to solve it. In the following illustration, I will use a 3*3 grid for demonstration, after we have understand it, we could extend it to size with any size.
First of all, the Lights status are represented with matrix L. Here 1 means the lights are on, 0 for off.
\[ L = \begin{vmatrix}
0 & 1 & 0 \\
1 & 1 & 0 \\
0 & 1 & 1
\end{vmatrix} \]
To make all the lights on, we should toggle some lights to generate effects of
\[ \overline{L} = \begin{vmatrix}
1 & 0 & 1 \\
0 & 0 & 1 \\
1 & 0 & 0
\end{vmatrix} \]
start from 0 matrix.
The action of the switch placed at (i,j) can be interpreted as the matrix ${A}_{ij}$ , where $A_{ij}$ is the matrix in which the only entries equal to 1 are those placed at (i,j) and in the adjacent positions; there are essentially three types of matrices ${A}_{ij}$, for different types of position (corner, edge, internal):
$${A}_{ij}= \begin{cases} \begin{vmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{vmatrix}& \text{if i,j refer to top-left corner light}\\ \begin{vmatrix} 1 & 1 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{vmatrix}& \text{if i,j refer to top-middle light}\\ \begin{vmatrix} 0 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 0 \end{vmatrix}& \text{if i,j refer to internal light}\\ \text{...}\\ \end{cases}$$Every winning combination of moves can be expressed mathematically in the form:
$$\sum_{i,j} {x_{ij} } { {A}_{ij} } = \overline{L}$$each coefficient $x_{ij}$ represents the number of times that switch (i,j) has to be pressed. According to our previous deduction, it could be only 1 or 0. And if we flatten the ${A}_{ij}$ into a vector, then we get the following equation:
$$\begin{vmatrix} 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 \end{vmatrix} \begin{vmatrix} {x_{11}} \\ {x_{12}} \\ {x_{13}} \\ {x_{21}} \\ {x_{22}} \\ {x_{23}} \\ {x_{31}} \\ {x_{32}} \\ {x_{33}} \\ \end{vmatrix} = \begin{vmatrix} 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \end{vmatrix}$$Pretty good, But how could we solve this equation? It’s not a traditional linear equation, it’s based on an (mod 2) operation or what we call “XOR”. But the basic idea is the same, we just redefine the operation like “add”, “multiply” and then compute the equation.
There is a lot of solution given in different languages, let’s take a look at a python version provided by pmneila. I add some comment in the code for a (hopefully) easier understanding.
1 | # coding: utf-8 |
run it and it give output like:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28$ python lightsout_solver.py
lights status:
[[1 0 1]
[0 0 1]
[1 0 0]]
inverse of matrix:
[[1 0 1 0 0 1 1 1 0]
[0 0 0 0 1 0 1 1 1]
[1 0 1 1 0 0 0 1 1]
[0 0 1 0 1 1 0 0 1]
[0 1 0 1 1 1 0 1 0]
[1 0 0 1 1 0 1 0 0]
[1 1 0 0 0 1 1 0 1]
[1 1 1 0 1 0 0 0 0]
[0 1 1 1 0 0 1 0 1]]
eigenvectors of matrix:
[]
The solution of
[[1 0 1]
[0 0 1]
[1 0 0]]
is
[[0 1 0]
[0 1 0]
[1 0 0]]
To solve this equation to get those coefficent $x_{ij} = 1$ , we get a solution $[x_{12}, x_{22}, x_{31}]$.
| X | O | X | O | X | O | O | O | O | O | O | O | |||
| O | O | X | switch (1,2) => | O | X | X | switch (2,2) => | X | O | O | switch (3,1) => | O | O | O |
| X | O | O | X | O | O | X | X | O | O | O | O |
Solution 3: Light Chasing
The above solution is effective, but it’s also crazy to ask someone to solve a equation with 25 parameters in a Room Escape Game. The following approach is easy to follow and to get the solution. The Principle of this solution is “normalize different boards into several solvable boards, and solved them with known strategies”.
Here is how it proceed:
- rows are manipulated one at a time starting with the top row. All the lights are turned on in the row by toggling the adjacent lights in the next row.
- apply the same method on 2-4 row.
- The last row is solved separately, depending on its active lights. Corresponding lights (see table below) in the top row are toggled and the initial algorithm is run again, resulting in a solution.
| Bottom row | switch Top row |
|---|---|
| XOOOX | XXOOO |
| OXOXO | XOOXO |
| XXXOO | OXOOO |
| OOXXX | OOOXO |
| XOXXO | OOOOX |
| OXXOX | XOOOO |
| XXOXX | OOXOO |
This approach always lead to an solution (if there is any) for a 5 * 5 Grid. This might be the ideal solution when trapped in the game :).